The process involves a considerable degree of subjectivity on the part of the patient in trying to describe his or her symptoms, and of the clinician whose final diagnosis will depend on his or her clinical experience and interpretation of what is normal and what is pathological.

Epidemiological studies can provide information not only on specific diagnostic entities but also on their underlying symptomatic constellations.

For this purpose, Sleep-EVAL was developed for the assessment of sleep and psychiatric disorders, endowed with the fuzzy logic capabilities necessary to determine the degree to which a given symptom corresponds to a specific diagnosis.

Inferential models of the probabilistic or fuzzy-logic type take into account such uncertainty.

Therefore, two incidences of uncertainty are very important:

• one in data collection and
• the other in diagnostic decision-making.

The manner in which these problems are tackled has a direct influence on what can be recognized and on how data analyses can be accomplished.

Inference models such as probabilistic and fuzzy systems can be used to integrate uncertainty in both symptomatic assessment and diagnostic attribution.
It therefore becomes possible to extend boundaries and attribute a degree of certainty to a diagnosis.
A probabilistic model can be easily computed from an existent binary data set.
A fuzzy model can also be calculated from an existent data set, but the model gains in precision if the data are expressed in categorical terms.
It should be noted that this model is more difficult to compute than the probabilistic model and requires the creation of a computer algorithm to calculate the degree of membership of each symptom involved in a diagnosis.
Nevertheless, this model is of greater interest than the probabilistic and binary models because it allows for a complete integration of the element of uncertainty in the process.

The inclusion of uncertainty in data should permit an improvement in classificatory systems such as DSM-IV and ICSD-90.
Indeed, weight and strength of the relationship between criteria within the same diagnosis can be improved, and at least the place of criteria within a certain category can be verified and eventually discarded.
For example, in a syndrome Y defined by the presence of criteria A, B, C, and D, a fuzzy model could show that a low weight on criterion A, accompanied by a strong weight on criteria B and C, and a moderate weight on D are enough to give a certainty of about 80% in the diagnosis.
This provides clues to the clinician that B and C are more relevant in the diagnosis and their presence should make suspect whether the diagnosis is present even if the other criteria have an uncertain presence.

This kind of result could validate classification and impart more legitimacy in their use in clinical practice and in pharmaceutical trials.

DIFFERENCES BETWEEN BINARY, PROBABILISTIC AND FUZZY MODELS

To reduce the uncertainty inherent in symptomatology assessment, a binary form is usually used to determine the presence or absence of a symptom.
However, this introduces another form of uncertainty especially in borderline cases where we must decide somehow whether a situation is normal or pathological.

An alternative is to use probabilistic modeling in order to change these boundaries.
This allows the creation of a natural framework that retains the characteristics of the diagnostic classification and can still be interpreted in the usual way.
Another possibility is to use fuzzy logic, which will afford a degree of certainty to the outcome.

The results of an epidemiological survey conducted in Italy will be used to illustrate the application of these methods.
This survey involved 3,970 subjects drawn from the non-institutionalized general population aged 15 to 99 years.

An extensive description of the epidemiological methodology can be found elsewhere (10).

FIRST EXAMPLE: INSOMNIA COMPLAINT

It performs a number of mathematical operations, such as converting age into months or weeks and hours into minutes or seconds, comparing duration of symptoms or discrepancies between hours, and setting the range of responses to be entered by numerical keypad.

FIRST EXAMPLE: INSOMNIA COMPLAINT

According to the DSM-IV criteria for insomnia used for the purpose of illustration, an insomnia complaint is defined as difficulty initiating or maintaining sleep or non-restorative sleep, lasting at least one month and accompanied by significant daytime repercussions in important areas of functioning.

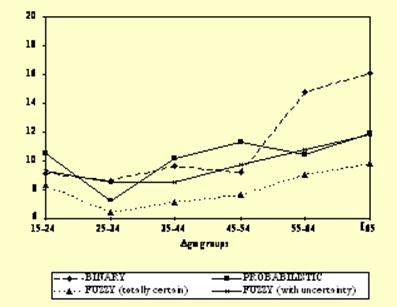In the probabilistic model, the diagnostic outcome (i.e., presence or absence of insomnia), is a function of symptom probabilities, as per Bayes theorem, the sum of which represents the prevalence estimate.
In the fuzzy model, the diagnostic outcome is expressed as a fuzzy set distributed over seven categories ranging from completely certain of presence to completely certain of absence.

The Figure shows the results for binary, probabilistic and fuzzy outcomes.

The overall prevalence of insomnia with the binary system was 10.8%, compared with 10.1% with the probabilistic model.

With the fuzzy model, 7.8% of the subjects were 100% certain of having insomnia and 1.8% were about an 80% certain, resulting in a prevalence of about 10.6%.

It can be seen that the probabilistic model had a leveling effect across age groups.
This could be the result of an unwanted reduction in the variation estimates, most notable when cells are based on few cases. The same occurred under the fuzzy model.

SECOND EXAMPLE: OBSTRUCTIVE SLEEP APNEA SYNDROME

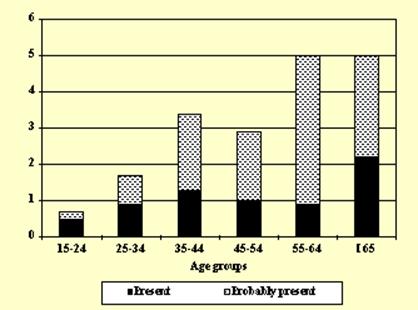
The second illustration involves Obstructive Sleep Apnea Syndrome (ICSD-90 classification).
Sleep-EVAL concluded with a complete certainty the presence of Obstructive Sleep Apnea Syndrome in 1.1% of the Italian sample and an almost certain presence in 1.9% (see figure 4 for the distribution by age groups).

In a study involving 105 patients from two sleep disorders centers (unpublished data), the same decisional tree yielded an almost perfect agreement (96.7% of agreement; kappa of 0.94) between Sleep-EVAL diagnosis (including the case when the system is not totally certain) and the diagnosis of sleep specialists confirmed with polysomnography.

Consequently, fuzzy logic reasoning can also offer the possibility of exploring prevalence of disorders in the general population using several levels of confidence.

Probabilistic models also offer different levels of confidence.
The main limitation relies on the calculation required to determine the different levels.
This first requires the determination of several levels of probability to have the disease X according different predetermined sets of criteria.
Prevalence estimates are then derived from these different probabilities.
Therefore, one can see that probabilistic models can only be done a posteriori, once all the data is collected.
The application of a fuzzy model does not require knowledge of probabilities.
Therefore, it can be applied a priori.
However, it requires great attention in the creation and application of fuzzy sets since these determine the correspondence between the data and the underlying concept.

CONCLUSIONS

The aim of a classification is to ensure a common language between the clinicians that use it, so that an entity such as "Psychophysiological Insomnia" refers to a symptomatology understood by any clinician familiar with the classification.

Matters, however, are complicated by the existence of multiple classifications, and clinicians can hardly be expected to be familiar with all of them.
The use of structured diagnostic tools is therefore necessary.
The clinician's clinical experience and theoretical background are major factors impacting on the final diagnosis.

Several studies have shown that clinicians do not make optimal use of classifications and often fail to properly document the underlying symptomatology (11,12).
This is further illustrated by the Buysse et al. study in five sleep disorder clinics (13) where no structured interview was used.
As a consequence, kappa coefficients were quite low between the sleep specialists (.30 for all listed diagnoses; .42 for cases of Insomnia Related to Another Mental Disorder) and there was a significant variability of kappa coefficients across the five experimentation sites.

The Sleep-EVAL system is designed to assess a variety of sleep disorders in the general population on the basis of two classificatory systems (i.e., DSM-IV and ICSD-90) and performs fuzzy reasoning.
Expert systems such as Sleep-Eval can be used to test classifications by assessing the symptomatic constellation underlying a diagnosis.

The use of Sleep-EVAL ensures that the full spectrum of the classification is covered, including rare diagnoses which do not necessarily receive the physician's immediate attention.
Sleep-EVAL also ensures that at least the minimal criteria for a diagnosis are present and makes it possible to explore the symptomatic constellations of specific diagnoses.
One of the main advantages of such modeling consist in the ability to verify how suitable existing classifications are for general populations.

Inference models such as probabilistic and fuzzy systems can be used to integrate uncertainty in both symptomatic assessment and diagnostic attribution.
It therefore becomes possible to extend boundaries and attribute a degree of certainty to a diagnosis.
A probabilistic model can be easily computed from an existent binary data set.

A fuzzy model can also be calculated from an existent data set, but the model gains in precision if the data are expressed in categorical terms.
It should be noted that this model is more difficult to compute than the probabilistic model and requires the creation of a computer algorithm to calculate the degree of membership of each symptom involved in a diagnosis.
Nevertheless, this model is of greater interest than the probabilistic and binary models because it allows for a complete integration of the element of uncertainty in the process.

The inclusion of uncertainty in data should permit an improvement in classificatory systems such as DSM-IV and ICSD-90.
Indeed, weight and strength of the relationship between criteria within the same diagnosis can be improved, and at least the place of criteria within a certain category can be verified and eventually discarded.
This kind of result could validate classification and impart more legitimacy in their use in clinical practice and in pharmaceutical trials.

REFERENCES

1. Ohayon MM. Improving decision making processes with the fuzzy logic approach in the epidemiology of sleep disorders. J Psychosom Res 1999 Oct;47(4):297-311